2.7.2.2. Cost-Benefit Analysis
Cost-benefit analysis (CBA) involves valuing all costs and benefits of a proposed
project over time on the basis of willingness to pay (or willingness to accept
compensation) on the part of project beneficiaries (affected people) and specifying
a decision criterion to accept or turn down the project (see Ray, 1984; Morgenstern,
1997). This criterion usually is the compensation principle, implying that those
who benefit from the project should be able to compensate the losers. The applicability
of CBA as a DAF for climate policy has been a fiercely debated issue. Although
the debate continues about the extent to which traditional CBA can provide useful
information for global-level decisionmaking, there is more agreement on its
usefulness in adaptation decisions at the national and regional scales.
In practical applications, all costs (C) and benefits (B) are defined as follows:
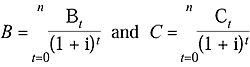
where i is the social discount rate, n is the project life, and
t denotes the year. One can use different cost-benefit criteria for ranking
projects or choosing the best among them: the cost-benefit ratio, CBR = B/C
> 1; the net present value, NPV = B - C > 0; and the internal
rate of return, IRR > i, where IRR is the discount rate to make B
= C. When we evaluate a single project, these criteria lead to the same
conclusion. In choosing the most desirable alternative, however, these criteria
indicate different orders of desirability.
A CBA in the adaptation context takes potential regional climate change scenarios
and their impacts as its starting point. The next step is to establish costs
of alternative adaptive measures as a function of their scales of application—the
marginal cost curve. A related task is to estimate how much damage can be averted
by increasing the adaptation effort—WTP (marginal benefit curve). The decision
principle suggests undertaking adaptive measures as long as marginal averted
damages (benefits) exceed marginal costs. This rule of thumb is easier to apply
in sectoral adaptation decisions, in which costs and benefits can be derived
from market prices. Difficulties arise in nonmarket sectors in which the valuation
behind the marginal cost and benefit curves often is debated. Difficulties multiply,
in a regional context, when costs and benefits must be aggregated across many
sectors.
A frequent critique of CBA and its applicability in adaptation studies is that
the underlying measurements are incomplete (especially in regional studies,
which do not cover all important aspects), inaccurate (even the costs and benefits
of adaptive actions included in the analysis are impossible to measure precisely),
and debated (related to the two preceding points; the inclusion and exact valuation
of many costs and benefits involve inherently subjective value judgments). These
criticisms are largely valid. However, it is still better to get at least the
measurable components right and complement them with a combination of judgments
on hard-to-measure items and sensitivity tests to assess their implications
than to abandon the whole method simply because it does not get everything perfect.
Nevertheless, it is important that users of these tools and their results fully
understand the limitations and confidence attached to them. Duke and Kammen
(1999) argue that accounting for dynamic feedback between the demand response
and price reductions from production experience can be used to account for deadweight
loss and other market dynamics that determine the benefit-cost ratio of economic
and policy measures to expand the market for clean energy technologies. These
results further support a broader role for market transformation programs to
commercialize new environmentally attractive technologies. The same dynamic
feedback processes also are relevant for CBA applications to adaptation decisions.
For example, consider changing precipitation patterns that would increase the
frequency of high-water conditions. Take flood-related damages as the function
of flood return periods: Annual flooding may cause the least damages, whereas
a 5-year return flood will cause somewhat more, a 20-year return flood even
more, and so on. Adaptation costs increase along the same axis because it takes
higher dikes and larger flood protection reservoirs to control a 50-year return
flood than a 5-year return flood. The level at which a given society will decide
to protect itself against floods depends on local economic conditions and geographical
and technological endowments. A CBA suggests that it should be in the neighborhood
of where marginal costs of additional flood protection would be equal to WTP
for additional flood protection.
|