9.7.1.1 Modeling the Impact of Climate Change on Malaria
Classical epidemiological models of infectious disease use the basic reproduction
rate, R0. This measure is defined as the number of new cases of a disease that
will arise from one current case when introduced into a nonimmune host population
during a single transmission cycle (Anderson and May, 1992). The basic reproduction
rate—or a related concept, "vectorial capacity"—can provide
a relative index of the impact of different climate scenarios on the transmissibility
of vector-borne diseases such as malaria. Vectorial capacity, however, is determined
by complex interactions of many host, vector, pathogen, and environmental factors.
Some of the variables are sensitive to temperature, including mosquito density,
feeding frequency, mosquito survival, and the extrinsic incubation period (EIP)
of the parasite (plasmodium) in the mosquito (Martens et al., 1999).
The EIP is especially important, and, within the lower temperature range, it
is very temperature-sensitive.
|
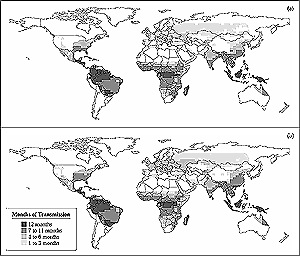 Figure
9-2: Potential impact of climate change on seasonal transmission of
falciparum malaria. Output from MIASMA v2.0 malaria model (Martens et
al., 1999) indicates the number of months per year when climate conditions
are suitable for falciparum transmission and where there is competent
mosquito vector: (a) months of potential transmission under current climate
(1961-1990); (b) months of potential transmission under a GHG-only
climate scenario (HadCM2 ensemble mean) in the 2080s. Future changes in
mosquito distributions are not modeled. This model does not take into
account control or eradication activities that have significantly limited
the distribution of malaria. Figure
9-2: Potential impact of climate change on seasonal transmission of
falciparum malaria. Output from MIASMA v2.0 malaria model (Martens et
al., 1999) indicates the number of months per year when climate conditions
are suitable for falciparum transmission and where there is competent
mosquito vector: (a) months of potential transmission under current climate
(1961-1990); (b) months of potential transmission under a GHG-only
climate scenario (HadCM2 ensemble mean) in the 2080s. Future changes in
mosquito distributions are not modeled. This model does not take into
account control or eradication activities that have significantly limited
the distribution of malaria.
|
Biological (or process-based) models have been used to
estimate the potential transmission of malaria. This is a measure of the extent
to which the natural world (the global environment-climate complex) would allow
the transmission of malaria if there were no other human-imposed constraints
on transmission. However, in some areas where human-imposed constraints have
occurred as a result of economic growth, or were put in place purposely, malaria
transmission has been successfully controlled, regardless of suitable local
temperatures. There has been considerable evolution of models since the SAR
(Martens et al., 1995, 1997, 1999; Martin and Lefebvre, 1995). One model
(Martens et al., 1999) includes vector-specific information regarding
the temperature-transmission relationship and mosquito distribution limits.
Recent studies using that revised model applied to the HadCM2 climate scenarios
project a global increase of 260-320 million people in 2080 living in the
potential transmission zone (against a baseline expectation of about 8 billion—that
is, a 2-4% increase in the number of people at risk) (Martens et al.,
1999; McMichael et al., 2000a). This projection, by design, does not
take into account the fact that much of this additional population at risk is
in middle- or high-income countries where human-imposed constraints on transmission
are greatest and where potential transmission therefore is unlikely to become
actual transmission. The model also projects regional increases and a few decreases
in the seasonal duration of transmission in current and prospective areas of
malaria transmission. Constraining of GHG emissions to achieve CO2 stabilization
within the range 550-750 ppm would reduce those projected increases by
about one-third (Arnell et al., 2001).
On a global scale, all biological models show net increases in the potential
transmission zone of malaria and changes in seasonal transmission under various
climate scenarios (Martens et al., 1995, 1999; Martin and Lefebvre, 1995).
Some local decreases in malaria transmission also are predicted to occur where
declines in rainfall would limit mosquito survival. The outputs of these malaria
models are very sensitive to assumptions about the minimum rainfall or humidity
levels needed for malaria transmission.
Another global modeling study (Rogers and Randolph, 2000) used a statistical-empirical
approach, in contrast to the aforementioned biological models. The outcome variable
in this model is the number of people living in an actual transmission zone,
as opposed to a potential transmission zone (as estimated by biological models).
Using an IS92a (unmitigated) climate scenario, this study estimated no significant
net change by 2080 in the portion of the world's population living in actual
malaria transmission zones; modeled malaria transmission increased in some areas
and decreased in others. This study made the assumption that the actual geographic
distribution of malaria in today's world is a satisfactory approximation
of its historical distribution prior to modern public health interventions.
This assumption is likely to have biased the estimation of the underlying multivariate
relationship between climatic variables and malaria occurrence because the sensitive
climate-malaria relationship in the lower temperature range in temperate zones
(especially Europe and the southern United States) would have been excluded
from the empirically derived equation. Hence, the use of that derived equation
to predict malaria risk in 2080 would have been relatively inert to marginal
climatic changes at the fringes of the current geographic distribution.
Another type of modeling addresses changes in the distribution of mosquito
vector species only. The CLIMEX model estimates changes in global and national
(Australia) distribution of malaria vectors under a range of climate scenarios,
based on the vectors' temperature and moisture requirements (Bryan et
al., 1996; Sutherst, 1998). The distribution of Anopheles gambiae complex
is projected to undergo a net increase in distribution in southern Africa under
three climate change scenarios (Hulme, 1996). However, these models do not address
complex ecological interactions, such as competition between species.
None of these models have been adequately validated at global or regional levels.
Modeling to date has not satisfactorily addressed regional vulnerability to
malaria or changes in risk in highland regions (Lindsay and Martens, 1998).
This is principally because it is difficult to obtain sufficiently detailed
geographic distribution maps of mosquitoes and malaria occurrence over time.
An important criticism of biological models is that undue emphasis is placed
on temperature changes, without consideration to other ecological complexities—including
those influenced by rainfall, humidity, and host exposure—that influence
transmission dynamics. Furthermore, the equations within a global model may
be inappropriate for particular local conditions, and there is a need for cross-validation
of large-scale and small-scale studies (Root and Schneider, 1995). Some attempts
to apply these integrated modeling techniques to smaller scale regional settings
have attempted to take account of local/regional conditions (Lindsay and Martens,
1998). None of the modeling to date has incorporated the modulating effect of
public health strategies and other social adaptive responses to current or future
malaria risk (Sutherst et al., 1998). Nevertheless, it remains a legitimate
and important question to estimate, under scenarios of climate change, change
in the extent to which the natural world (the global environment-climate complex)
would allow transmission of malaria if there were no other human-imposed constraints
on transmission.
|