3.5.5 Regional Differences
|
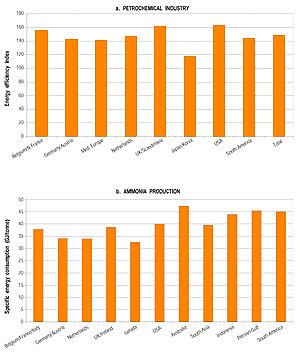
Figure 3.13a-b: Relative levels of energy efficiency for selected
industrial sectors in various countries. The aggregate energy efficiency
index (EEI) is calculated as: EEI = (Si Pi ·SECi)/(
Si Pi · SECi,BP), where Pi
is the production volume of product i; SECi is the specific
energy consumption for product i, and SECi,BP is a best-practice
reference level for the specific energy consumption for product i. By
applying this approach a correction is made in order to account for structural
differences between countries in each of the tracked industrial sectors.
A typical statistical uncertainty for these figures is 5%. Because of
statistical errors higher uncertainties may occur in individual cases.
|
|
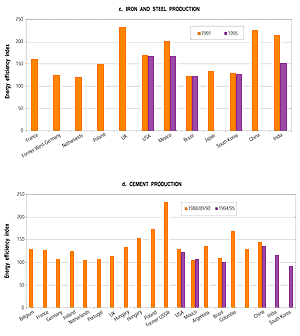
Figure 3.13c-d: Relative levels of energy efficiency for selected
industrial sectors in various countries. The aggregate energy efficiency
index (EEI) is calculated as: EEI = (Si Pi ·SECi)/(
Si Pi · SECi,BP), where Pi
is the production volume of product i; SECi is the specific
energy consumption for product i, and SECi,BP is a best-practice
reference level for the specific energy consumption for product i. By
applying this approach a correction is made in order to account for structural
differences between countries in each of the tracked industrial sectors.
A typical statistical uncertainty for these figures is 5%. Because of
statistical errors higher uncertainties may occur in individual cases.
|
|
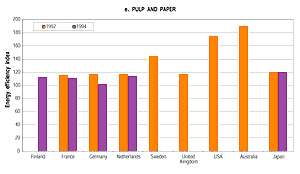
Figure 3.13e: Relative levels of energy efficiency for selected
industrial sectors in various countries. The aggregate energy efficiency
index (EEI) is calculated as: EEI = (Si Pi ·SECi)/(
Si Pi · SECi,BP), where Pi
is the production volume of product i; SECi is the specific
energy consumption for product i, and SECi,BP is a best-practice
reference level for the specific energy consumption for product i. By
applying this approach a correction is made in order to account for structural
differences between countries in each of the tracked industrial sectors.
A typical statistical uncertainty for these figures is 5%. Because of
statistical errors higher uncertainties may occur in individual cases.
|
Differences in emission reduction potential are mainly caused by differences
in specific energy consumption of industrial processes. In recent years attention
was paid to developing methods to compare energy efficiency levels on a physical
basis (Phylipsen et al., 1998a), in addition to methods that compare energy
efficiency levels on a monetary basis (see, e.g., Schipper and Meyers, 1992).
Energy efficiency indicators on a physical basis start from the level of energy
consumption per unit of product (e.g., expressed in GJ/t). However, countries
may differ in the production structure per sector (i.e. differences in product
mix and associated differences in feedstocks used). Correction for such differences
can take place by relating the specific energy consumption level for each product
to a best practice level, resulting in a so-called energy efficiency index.
The more efficient the aggregate of processes in a sector in a country, the
lower the energy efficiency index. The energy efficiency indices are scaled
in such a way that if all processes were operated at the best-practice level,
the index would be 100.
Results up to now are presented in Figure 3.13. Apart
from correction for structure, international comparison of energy efficiency
requires correction for statistical errors. A common source of error in the
process industries is the double counting of fuels (e.g., in the iron and steel
industry double counting of coke input to the blast furnace and blast furnace
gas). After correction for such errors the energy efficiency indicators –
like those presented in Table 3.19 – show
a typical uncertainty of 5% (Farla, 2000).
Despite the remaining uncertainties, some conclusions can be drawn from these
data. In general Japan and South Korea and countries in Western Europe show
the lowest energy efficiency index (i.e., they are most efficient). Developing
countries, economies in transition and some OECD countries (like the USA and
Australia) show higher levels of this index. However, there are certainly exceptions;
for instance, some developing countries show fairly low levels of the energy
efficiency index for some sectors. This may be explained by the fact that these
countries are developing at a high rate, and hence apply relatively young and
modern technology. In general the countries with the highest energy efficiency
index will have the highest technical potential for energy efficiency improvement.
The differences in economic potential may be smaller, as a consequence of the
lower energy prices that often occur in the less efficient countries. In this
section a number of regional studies – mainly into energy efficiency in
industry – are reviewed.
3.5.5.1 China
Industry is responsible for 75% of commercial energy end-use in China (IEA,
1997d). The period from 1980 to 1996 has seen a strong economic growth and growth
of industrial production, but also a substantial decline of the energy/GDP ratio
of about 4% per year (China Statistical Yearbook). The share of energy efficiency
and structural change in this decline is uncertain, but it is clear that substantial
energy efficiency improvement was obtained (Zhou and Hu, 1999; Sinton, 1996).
Nevertheless, Chinese industry is still substantially less energy efficient
than most OECD countries (Wu and Wei, 1997), see also Figure
3.13. Within industry, the steel industry is most important, consuming 23%
of industrial energy use in 1995 (IEA, 1997d). Zhou and Hu (1999) analysed the
differences between the Chinese and the efficient Japanese iron and steel industry
and identified a range of measures to improve the specific energy consumption
of the Chinese steel industry. Important measures are the recovery of residual
gases (2.7GJ/t steel); boiler modification and CHP (2.1 GJ/t); improved feedstock
quality (2.1GJ/t); wider application of continuous casting (1.0GJ/t); and others
(2.0GJ/t). The total leads to a reduction of 25% compared to the present average
of 35.6GJ/t (Zhou and Hu, 1999). An analysis of future prospects by Worrell
(1995) shows that, in the case steel production grows from 93Mt in 1995 to 140Mt
in 2020, energy consumption in the Chinese steel industry is likely to grow.
But the growth can be very moderate if modern technologies, like smelt reduction
and near-net-shape casting, are adopted. Also for two other important sectors,
the building materials industry and the chemical industries, substantial technical
saving potentials are reported (Zhou and Hu, 1999). Liu et al. (1995) report
for the cement industry – consuming 10% of industrial energy use in 1995
– a potential for reduction of the specific energy consumption of 32% in
the period 1990 to 2000; associated investments are estimated at 105 billion
yuan (~US$13 billion). Important economically viable options are comprehensive
retrofit of vertical kilns (e.g., improving refractory lining) and wet kilns,
and kiln diameter enlargement and retrofit. Similar savings can be reached when
adding a pre-calciner to the kilns, which is, however, the most expensive option.
All cost-effective measures add up to a 20% reduction of primary energy consumption
compared to the base line energy use in 2010 (Sinton and Yang, 1998).
3.5.5.2 Japan
In Japan, industry accounts for nearly half of the final energy demand. Industrial
energy demand is stabilizing, mainly because of the shift from heavy industry
to sectors like electrical machinery, precision instruments, and motor vehicles.
Substantial energy efficiency improvements have been obtained, and Japan is
now one of the most efficient countries in the world (see also Figure
3.13). Nevertheless, there are still energy efficiency improvement potentials.
Current technical potential is 10%–12% in the iron and steel industry.
Under the influence of a carbon tax, the potential is 8% in the cement industry
and 10% in the chemical industry. Costs of saving energy are in the majority
of the cases lower than energy purchase costs at a 5% discount rate (Kashiwagi
et al., 1999). Kainuma et al. (1999) have carried out an analysis of various
policies using the AIM model and find maximum absolute reductions of industrial
CO2 emissions of 15% (in the base case the absolute emission reduction
is 3%). The increasing concern about the climate change issue has required setting
a new higher target to curb energy use to the FY 1996 level in FY 2010, which
requires an energy savings of approximately 10% of final demand in the industrial
sector by the revision of the Energy Conservation Law put into force in April
1999 (MITI, 1999).
|