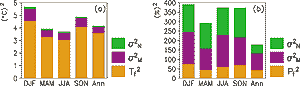
Figure 9.4: Intercomparison statistics for seasonal and annual (a) temperature and (b) precipitation changes in nineteen CMIP2 experiments at the doubling of CO2 (years 61 to 80). The total length of the bars shows the mean squared amplitude of the simulated local temperature and precipitation changes averaged over all experiments and over the whole world. The lowermost part of each bar represents a nominally unbiased “common signal”, the mid-part directly model-related variance and the top part the inter-experiment variance attributed to internal variability. Precipitation changes are defined as 100% x (PG-PCTRL) / Max(PCTRL, 0.25 mm/day), where the lower limit of 0.25 mm/day is used to reduce the sensitivity of the global statistics to areas with very little control run precipitation.

Since the SAR, there have been a number of new AOGCM climate simulations with various forcings that can provide estimates of possible future climate change as discussed in Section 9.1.2. For the first time we now have a reasonable number of climate simulations with different forcings so we can begin to quantify a mean climate response along with a range of possible outcomes. Here each model’s simulation of a future climate state is treated as a possible outcome for future climate as discussed in the previous section.

These simulations fall into three categories (Table 9.1):

• The first are integrations with idealised forcing, namely, a 1%/yr compound increase of CO₂. This 1% increase represents equivalent CO₂, which includes other greenhouse gases like methane, NO_x etc. as discussed in Section 9.2.1. These runs extend at least to the time of effective CO₂ doubling at year 70, and are useful for direct model intercomparisons since they use exactly the same forcing and thus are valuable to calibrate model response. These experiments are collected in the CMIP exercise (Meehl et al., 2000a) and referred to as “CMIP2” (Table 9.1).
• A second category of AOGCM climate model simulations uses specified time-evolving future forcing where the simulations start sometime in the 19th century, and are run with estimates of observed forcing through the 20th century (see Chapter 8). That state is subsequently used to begin simulations of the future climate with estimated forcings of greenhouse gases (“G”) or with the additional contribution from the direct effect of sulphate aerosols (“GS”) according to various scenarios, such as IS92a (see Chapter 1). These simulations avoid the cold start problem (see SAR) present in the CMIP experiments. They allow evaluation of the model climate and response to forcing changes that could be experienced over the 21st century. The experiments are collected in the IPCC-DDC. These experiments are assessed for the mid-21st century when most of the DDC experiments with sulphate aerosols finished.
• A third category are AOGCM simulations using as an initial state the end of the 20th century integrations, and then following the A2 and B2 (denoted as such in Table 9.1) draft marker SRES forcing scenarios to the year 2100 (see Section 9.1.2). These simulations are assessed to quantify possible future climate change at the end of the 21st century, and also are treated as members of an ensemble to better assess and quantify consistent climate changes. A simple model is also used to provide estimates of global temperature change for the end of the 21st century from a greater number of the SRES forcing scenarios.

Table 9.1 gives a detailed overview of all experiments assessed in this report.

9.3.1.1 1%/yr CO₂ increase (CMIP2) experiments

Figure 9.3 shows the global average temperature and precipitation changes for the nineteen CMIP2 simulations. At the time of CO₂ doubling at year 70, the 20-year average (years 61 to 80) global mean temperature change (the transient climate response TCR; see Section 9.2) for these models is 1.1 to 3.1°C with an average of 1.8°C and a standard deviation of 0.4°C (Figure 9.7). This is similar to the SAR results (Figure 6.4 in Kattenberg et al., 1996).

At the time of CO₂ doubling at year 70, the 20-year average (years 61 to 80) percentage change of the global mean precipitation for these models ranges from -0.2 to 5.6% with an average of 2.5% and a standard deviation of 1.5%. This is similar to the SAR results.

For a hypothetical, infinite ensemble of experiments, in which T_m and T'' are uncorrelated and both have zero means,

{T²} = T_f² + {T_m²} + {T''²} = T_f²+ ²_M + ²_N.

The ensemble mean square climate change is thus the sum of contributions from the common forced component (T_f2), model differences (²_M), and internal variability (²_N ). This framework is applied to the CMIP2 experiments in Figure 9.4. These components of the total change are estimated for each grid box separately, using formulas that allow for unbiased estimates of these when a limited number of experiments are available (Räisänen 2000, 2001). The variance associated with internal variability 2N is inferred from the temporal variability of detrended CO₂ run minus control run differences and the model-related variance 2M as a residual. Averaging the local statistics over the world, the relative agreement between the CMIP2 experiments is much higher for annual mean temperature changes (common signal makes up 86% of the total squared amplitude) than for precipitation (24%) (Figure 9.4).

The relative agreement on seasonal climate changes is slightly lower, even though the absolute magnitude of the common signal is in some cases larger in the individual seasons than in the annual mean. Only 10 to 20% of the inter-experiment variance in temperature changes is attributable to internal variability, which indicates that most of this variance arises from differences between the models themselves. The estimated contribution of internal variability to the inter-experiment variance in precipitation changes is larger, from about a third in the annual mean to about 50% in individual seasons. Thus there is more internal variability and model differences and less common signal indicating lower reliability in the changes of precipitation compared to temperature.

IPCC Homepage