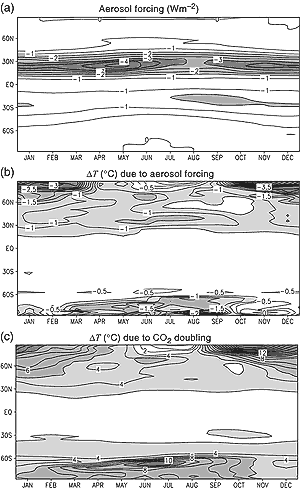
Figure 12.3: Latitude-month plot of radiative forcing and model equilibrium response for surface temperature. (a) Radiative forcing (Wm-2) due to increased sulphate aerosol loading at the time of CO2 doubling. (b) Change in temperature due to the increase in aerosol loading. (c) Change in temperature due to CO2 doubling. Note that the patterns of radiative forcing and temperature response are quite different in (a) and (b), but that the patterns of large-scale temperature responses to different forcings are similar in (b) and (c). The experi-ments used to compute these fields are described by Reader and Boer (1998).

The global mean change in radiative forcing (see Chapter 6) since the pre-industrial period may give an indication of the relative importance of the different external factors influencing climate over the last century. The temporal and spatial variation of the forcing from different sources may help to identify the effects of individual factors that have contributed to recent climate change.

The need for climate models
To detect the response to anthropogenic or natural climate forcing in observations, we require estimates of the expected space-time pattern of the response. The influences of natural and anthropogenic forcing on the observed climate can be separated only if the spatial and temporal variation of each component is known. These patterns cannot be determined from the observed instrumental record because variations due to different external forcings are superimposed on each other and on internal climate variations. Hence climate models are usually used to estimate the contribution from each factor. The models range from simpler energy balance models to the most complex coupled atmosphere-ocean general circulation models that simulate the spatial and temporal variations of many climatic parameters (Chapter 8).

The models used
Energy balance models (EBMs) simulate the effect of radiative climate forcing on surface temperature. Climate sensitivity is included as an adjustable parameter. These models are computationally inexpensive and produce noise-free estimates of the climate signal. However, EBMs cannot represent dynamical components of the climate signal, generally cannot simulate variables other than surface temperature, and may omit some of the important feedback processes that are accounted for in more complex models. Most detection and attribution approaches therefore apply signals estimated from coupled Atmosphere Ocean General Circulation Models (AOGCMs) or atmospheric General Circulation Models (GCMs) coupled to mixed-layer ocean models. Forced simulations with such models contain both the climate response to external forcing and superimposed internal climate variability. Estimates of the climate response computed from model output will necessarily contain at least some noise from this source, although this can be reduced by the use of ensemble simulations. Note that different models can produce quite different patterns of response to a given forcing due to differences in the representation of feedbacks arising from changes in cloud (in particular), sea ice and land surface processes.

The relationship between patterns of forcing and response
There are several reasons why one should not expect a simple relationship between the patterns of radiative forcing and temperature response. First, strong feedbacks such as those due to water vapour and sea ice tend to reduce the difference in the temperature response due to different forcings. This is illustrated graphically by the response to the simplified aerosol forcing used in early studies. The magnitude of the model response is largest over the Arctic in winter even though the forcing is small, largely due to ice-albedo feedback. The large-scale patterns of change and their temporal variations are similar, but of opposite sign, to that obtained in greenhouse gas experiments (Figure 12.3, see also Mitchell et al., 1995a). Second, atmospheric circulation tends to smooth out temperature gradients and reduce the differences in response patterns. Similarly, the thermal inertia of the climate system tends to reduce the amplitude of short-term fluctuations in forcing. Third, changes in radiative forcing are more effective if they act near the surface, where cooling to space is restricted, than at upper levels, and in high latitudes, where there are stronger positive feedbacks than at low latitudes (Hansen et al., 1997a).

In practice, the response of a given model to different forcing patterns can be quite similar (Hegerl et al., 1997; North and Stevens, 1998; Tett et al., 1999). Similar signal patterns (a condition often referred to as “degeneracy”) can be difficult to distinguish from one another. Tett et al. (1999) find substantial degeneracy between greenhouse gas, sulphate, volcanic and solar patterns they used in their detection study using HadCM2. On the other hand, the greenhouse gas and aerosol patterns generated by ECHAM3 LSG (Hegerl et al., 2000) are more clearly separable, in part because the patterns are more distinct, and in part because the aerosol response pattern correlates less well with ECHAM3 LSG’s patterns of internal variability. The vertical patterns of temperature change due to greenhouse gas and stratospheric ozone forcing are less degenerate than the horizontal patterns.

Summary
Different models may give quite different patterns of response for the same forcing, but an individual model may give a surprisingly similar response for different forcings. The first point means that attribution studies may give different results when using signals generated from different models. The second point means that it may be more difficult to distinguish between the response to different factors than one might expect, given the differences in radiative forcing.

IPCC Homepage