|
Appendix 12.1: Optimal Detection is Regression
The detection technique that has been used in most “optimal detection” studies
performed to date has several equivalent representations (Hegerl and North,
1997; Zwiers, 1999). It has recently been recognised that it can be cast as
a multiple regression problem with respect to generalised least squares (Allen
and Tett, 1999; see also Hasselmann, 1993, 1997) in which a field of n
“observations” y is represented as a linear combination of signal patterns
g1,...,gm plus noise u
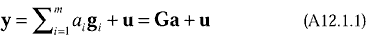
where G=(g1|...|gm) is the matrix composed of
the signal patterns and a=(a1,...,am)T
is the vector composed of the unknown amplitudes. The field usually contains
temperature observations, arrayed in space, either at the surface as grid box
averages of surface temperature observations (typically 5 5
degrees; Santer et al., 1995; Hegerl et al., 1997; Tett et al., 1999), or in
the vertical as zonal averages of radiosonde observations (Karoly et al., 1994;
Santer et al., 1996a; Allen and Tett, 1999). The fields are masked so that they
represent only those regions with adequate data. The fields may also have a
time dimension (Allen and Tett, 1999; North and Stevens; 1998; Stevens and North,
1996). Regardless of how the field is defined, its dimension n (the total number
of observed values contained in any one single realisation of the field) is
large. The signal patterns, which are obtained from climate models, and the
residual noise field, have the same dimension. The procedure consists of efficiently
estimating the unknown amplitudes a from observations and testing the
null hypotheses that they are zero. In the event of rejection, testing the hypothesis
that the amplitudes are unity for some combination of signals performs the attribution
consistency test. This assumes, of course, that the climate model signal patterns
have been normalised. When the signal is noise-free, estimates of the amplitudes
are given by 5
degrees; Santer et al., 1995; Hegerl et al., 1997; Tett et al., 1999), or in
the vertical as zonal averages of radiosonde observations (Karoly et al., 1994;
Santer et al., 1996a; Allen and Tett, 1999). The fields are masked so that they
represent only those regions with adequate data. The fields may also have a
time dimension (Allen and Tett, 1999; North and Stevens; 1998; Stevens and North,
1996). Regardless of how the field is defined, its dimension n (the total number
of observed values contained in any one single realisation of the field) is
large. The signal patterns, which are obtained from climate models, and the
residual noise field, have the same dimension. The procedure consists of efficiently
estimating the unknown amplitudes a from observations and testing the
null hypotheses that they are zero. In the event of rejection, testing the hypothesis
that the amplitudes are unity for some combination of signals performs the attribution
consistency test. This assumes, of course, that the climate model signal patterns
have been normalised. When the signal is noise-free, estimates of the amplitudes
are given by
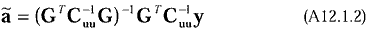
where Cuu is the n n
covariance matrix of the noise (Hasselmann, 1997, 1998; Allen and Tett, 1999;
Levine and Berliner, 1999). Generalisations allow for the incorporation of signal
uncertainties (see, for example, Allen et al., 2000b). A schematic two-dimensional
example is given in Box 12.1. In essence, the amplitudes
are estimated by giving somewhat greater weight to information in the low variance
parts of the field of observations. The uncertainty of this estimate, expressed
as the m n
covariance matrix of the noise (Hasselmann, 1997, 1998; Allen and Tett, 1999;
Levine and Berliner, 1999). Generalisations allow for the incorporation of signal
uncertainties (see, for example, Allen et al., 2000b). A schematic two-dimensional
example is given in Box 12.1. In essence, the amplitudes
are estimated by giving somewhat greater weight to information in the low variance
parts of the field of observations. The uncertainty of this estimate, expressed
as the m m covariance
matrix of Caa of ã, is given by m covariance
matrix of Caa of ã, is given by

This leads to a (1- ) ) 100%
confidence ellipsoid for the unknown amplitudes when u is the multivariate Gaussian
that is given by 100%
confidence ellipsoid for the unknown amplitudes when u is the multivariate Gaussian
that is given by
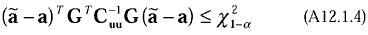
where 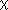 21- 21- is the (1-
is the (1- ) critical value
of the chi-squared distribution with m degrees of freedom. Marginal confidence
ellipsoids can be constructed for subsets of signals simply by removing the
appropriate rows and columns from GTC-1uuG
and reducing the number of degrees of freedom. The marginal (1- ) critical value
of the chi-squared distribution with m degrees of freedom. Marginal confidence
ellipsoids can be constructed for subsets of signals simply by removing the
appropriate rows and columns from GTC-1uuG
and reducing the number of degrees of freedom. The marginal (1- ) ) 100%
confidence interval for the amplitude of signal i (i.e., the confidence
interval that would be obtained in the absence of information about the other
signals) is given by 100%
confidence interval for the amplitude of signal i (i.e., the confidence
interval that would be obtained in the absence of information about the other
signals) is given by
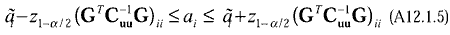
where Z1- /2
is the (1- /2
is the (1- /2) critical value
for the standard normal distribution. Signal i is said to be detected at the /2) critical value
for the standard normal distribution. Signal i is said to be detected at the
 /2 /2 100%
significance level if the lower limit confidence interval (A12.1.5)
is greater than zero. However, “multiplicity” is a concern when making inferences
in this way. For example, two signals that are detected at the 100%
significance level if the lower limit confidence interval (A12.1.5)
is greater than zero. However, “multiplicity” is a concern when making inferences
in this way. For example, two signals that are detected at the  /2 /2 100%
significance level may not be jointly detectable at this level. The attribution
consistency test is passed when the confidence ellipsoid contains the vector
of units (1,...,1)T. 100%
significance level may not be jointly detectable at this level. The attribution
consistency test is passed when the confidence ellipsoid contains the vector
of units (1,...,1)T.
|