|
12.4 Quantitative Comparison of Observed and Modelled Climate Change
A major advance since the SAR has been the increase in the range of techniques
used to assess the quantitative agreement between observed and modelled climate
change, and the evaluation of the degree to which the results are independent
of the assumptions made in applying those techniques (Table
12.1). Also, some studies have based their conclusions on estimates of the
amplitude of anthropogenic signals in the observations and consideration of
their consistency with model projections. Estimates of the changes in forcing
up to 1990 used in these studies, where available, are given in Table
12.2. In this section we assess new studies using a number of techniques,
ranging from descriptive analyses of simple indices to sophisticated optimal
detection techniques that incorporate the time and space-dependence of signals
over the 20th century.
| Table 12.1: Summary of the main detection and attribution
studies considered. |
 |
| Study |
Signals |
Signal source |
Noise source |
Method |
S, V |
Sources of uncertainty |
Time-scale |
No. of patterns |
Detect |
 |
| Santer et al., 1996 |
G, GS, O etc. |
Equilibrium / future LLNL, GFDL R15, HadCM2 |
GFDL R15, HadCM2, ECHAM1 |
F, Corr |
V |
Internal variability |
25 year Annual and seasonal |
1 |
GSO |
| Hegerl, 1996, 1997 |
G, GS |
Future ECHAM3, HadCM2 |
GFDL R15, ECHAM1, HadCM2; observation |
F, Pattern |
S |
Internal variability |
30, 50 years Annual and JJA |
1, 2 |
G, GS, S |
| Tett et al., 1996 |
G, GS, GSO |
Historical HadCM2 |
HadCM2 |
F, Corr |
V |
Internal variability |
35 years |
1 |
GSO |
| Hegerl et al., 2000 |
G, GS, Vol, Sol |
Future, ECHAM3, HadCM2 |
ECHAM3, HadCM2 |
F, Pattern |
S |
Internal variability; model uncertainty |
30, 50 years Annual and JJA |
1, 2 |
GS, G, S (not all cases) |
| Allen and Tett, 1999 |
G, GS, GSO |
Historical HadCM2 |
HadCM2 |
F, pattern |
V |
Internal variability |
35 years Annual |
1, 2 |
GSO and also G |
Tett et al., 1999
Stott et al., 2001 |
G,GS, Sol, Vol |
Historical HadCM2 |
HadCM2 |
Timespace |
S |
Internal variability, 2 solar signals |
50 years decadal and seasonal |
2 or more |
G, GS, Sol (Vol) |
North and Stevens, 1998
Leroy, 1998 |
G, GS, Sol, Vol |
Historical EBM |
GFDL ECHAM1, EBM |
Freq-Space |
S |
Internal variability |
Annual and hemispheric summer |
4 |
G, S, Vol |
| North and Wu, 2001 |
|
|
Same+Had CM2 |
Timespace |
|
|
Annual |
|
G, Vol |
| Barnett et al., 1999 |
G, GS, GSIO Sol+vol |
Future ECHAM3, ECHAM4, HadCM2, GFDL R15 |
ECHAM3, ECHAM4, HadCM2, GFDL R15 |
F, Pattern |
S |
Observed sampling error, model uncertainty, internal variability |
50 years JJA trends |
2 |
GS, G, S (S not all cases) |
| Hill et al., 2001 |
G, GSO,Sol |
Historical HadCM2 |
HadCM2 |
F, pattern |
V |
Internal variability |
35 years annual |
3 |
G |
| Tett et al., 2000 |
G,GSTI, GSTIO, Nat |
Historical HadCM3 |
HadCM3 |
Timespace |
S |
Internal variability |
50, 100 years decadal |
2 or more |
G, SIT, GSTIO and Nat |
| |
|
|
|
F, pattern |
V |
Internal variability |
35 years, annual |
2 |
GSTI |
 |
We begin in Section 12.4.1 with a brief discussion of
detection studies that use simple indices and time-series analyses. In Section
12.4.2 we discuss recent pattern correlation studies (see Table
12.1) that assess the similarity between observed and modelled climate changes.
Pattern correlation studies were discussed extensively in the SAR, although
subsequently they received some criticism. We therefore also consider the criticism
and studies that have evaluated the performance of pattern correlation techniques.
Optimal detection studies of various kinds are assessed in Section
12.4.3. We consider first studies that use a single fixed spatial signal
pattern (Section 12.4.3.1) and then studies that
simul-taneously incorporate more than one fixed signal pattern (Section
12.4.3.2). Finally, optimal detection studies that take into account temporal
as well as spatial variations (so-called space-time techniques) are assessed
in Section 12.4.3.3.
| Table 12.2: Estimated forcing from pre-industrial
period to 1990 in simulations used in detection studies (Wm-2).
GS indicates only direct sulphate forcing included, GSI indicates both direct
and indirect effects included. Other details of the detection studies are
given in Table 12.1. Details of the models are given
in Chapter 8, Table 8.1. |
 |
| Model |
Aerosol |
Baseline forcing |
1990 aerosol forcing |
1990 greenhouse gas forcing |
Source of estimate |
 |
| HadCM2 |
GS |
1760 |
-0.6 |
1.9 |
Mitchell and Johns, 1997 |
| HadCM3 |
GSI |
1860 |
-1.0 |
2.0 |
Tett et al., 2000 |
| ECHAM3/LSG |
GS |
1880 |
-0.7 |
1.7 |
Roeckner |
| ECHAM4/OPYC |
GSI |
1760 |
-0.9 |
2.2 |
Roeckner et al., 1999 |
| GFDL_R30 |
GS |
1760 |
-0.6 |
2.1 |
Stouffer |
| CGCM1,2 |
GS |
1760 |
~ -1.0 |
~2.2 |
Boer et al., 2000a,b |
 |
We provide various aids to the reader to clarify the distinction between the
various detection and attribution techniques that have been used. Box
12.1 in Section 12.4.3 provides a simple intuitive
description of optimal detection. Appendix 12.1 provides
a more technical description and relates optimal detection to general linear
regression. The differences between fixed pattern, space-time and space-frequency
optimal detection methods are detailed in Appendix 12.2
and the relationship between pattern correlation and optimal detection methods
is discussed in Appendix 12.3. Dimension reduction, a
necessary part of optimal detection studies, is discussed in Appendix
12.4.
|
Box 12.1: Optimal detection
Optimal detection is a technique that may help to provide a clearer separation
of a climate change fingerprint from natural internal climate variations.
The principle is sketched in Figure 12.B1, below (after Hasselmann, 1976).
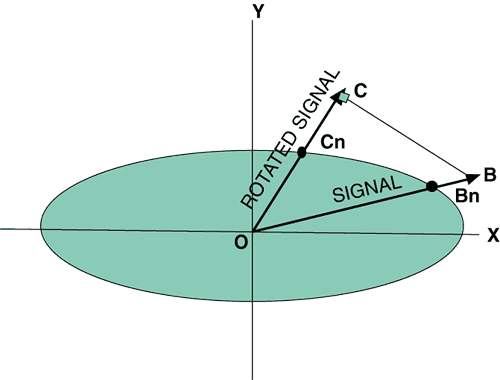
Suppose for simplicity that most of the natural variability can be described
in terms of two modes (well-defined spatial patterns) of variability.
In the absence of climate change, the amplitudes of these two modes, plotted
on a 2D diagram along OX and OY will vary with time, and for a given fraction
of occasions (usually chosen as 95%), the amplitude of each mode will
lie within the shaded ellipse. Suppose we are attempting to detect a fingerprint
that can be made up of a linear combination of the two patterns such that
it lies along OB. The signal to noise ratio is given by OB/OBn. Because
our signal lies close to the direction of the main component of variability,
the signal to noise ratio is small. On the other hand, we can choose a
direction OC that overlaps less with the main component of natural variability
such that the signal to noise ratio OC/OCn for the component of the signal
that lies in direction OC is larger even though the projected signal OC
is smaller then the full signal OB. Optimal detection techniques merely
choose the direction OC that maximises the signal to noise ratio. This
is equivalent to general linear regression (see Appendix
12.1). A good estimate of natural internal variability is required
to optimise effectively.
|
|