13.5.2.3 Risk assessment approaches
Uncertainty analysis is required to perform quantitative risk or decision analysis
(see Toth and Mwandosya (2001) for discussion of decision analysis). By itself,
scenario analysis is not equivalent to uncertainty analysis because not all
possible scenarios are necessarily treated and, especially, because probabilities
are not attached to each scenario (see Morgan and Henrion (1990) for a general
treatment of uncertainty analysis; see Katz (2000) for a more recent overview
focusing on climate change). Recognising this limitation, a few recent studies
(Jones, 2000b; New and Hulme, 2000) have attempted to modify climate scenario
analysis, grouping a range of scenarios together and attaching a probability
to the resultant classes. Such an approach can be viewed as a first step in
bridging the gap between scenario and uncertainty analysis. Single climate scenarios,
by definition, are limited to plausibility with no degree of likelihood attached.
Since risk analysis requires that probabilities be attached to each climate
scenario, subjective probabilities can be applied to the input parameters that
determine the climate outcomes (e.g., emissions scenarios, the climate sensitivity,
regional climate response patterns), thus allowing distributions of outcomes
to be formally quantified.
In formal risk analysis, the extremes of the probability distribution should
encompass the full range of possible outcomes, although in climate change studies
this remains hard to achieve. The ranges for global warming and sea level rise
from the IPCC WGI Second Assessment Report (IPCC, 1996) (hereafter SAR), for
example, deliberately did not encompass the full range of possible outcomes
and made no reference to probability distributions. As a consequence, the bulk
of impact assessments have treated these IPCC ranges as having a uniform probability,
i.e., acting as if no information is available about what changes are more likely
than others. As pointed out by Titus and Narayanan (1996), Jones (1998, 2000a),
and Parkinson and Young (1998), however, where several sources of uncertainty
are combined, the resulting probability distribution is not uniform but is a
function of the component probability distributions and the relationship between
the component elements. For example, descriptions of regional changes in temperature
and rainfall over Australia constructed from regional response patterns have
been used in a number of hydrological studies where the extreme outcomes have
been considered as likely as outcomes in the centre of the range (e.g., Chiew
et al., 1995; Schreider et al., 1996; Whetton, 1998). However, when the two
component ranges - global warming and normalised local temperature and rainfall
change -are randomly sampled and then multiplied together, they offer a distinctly
non-uniform distribution (see Figure 13.9a). Further refinements
of these approaches for quantifying the risk of climate change are needed (New
and Hulme, 2000).
This approach to portraying uncertainty has potentially useful applications
when combined with climate impact sensitivity response surfaces (see Section
13.2.1; see also Chapter 3 of TAR
WG II (Carter and La Rovere, 2001)). The superimposed response surfaces
allow the calculation of probabilities for exceeding particular impact thresholds
(Figure 13.9b). Another method of assessing risk using
quantified probability distributions is through a series of linked models such
as those used for calculating sea level rise (Titus and Narayanan, 1996) and
economic damage due to sea level rise (Yohe and Schlesinger, 1998), for quantifying
climate uncertainty (Visser et al., 2000), and in integrated assessments (Morgan
and Dowlatabadi, 1996). Efforts to make explicit probabilistic forecasts of
the climate response to a given emissions scenario for the near future have
been made using the current observed climate trajectory to constrain the “forecasts”
from several GCMs (Allen et al., 2000). More details on this technique are given
in Section 12.4.3.3.
|
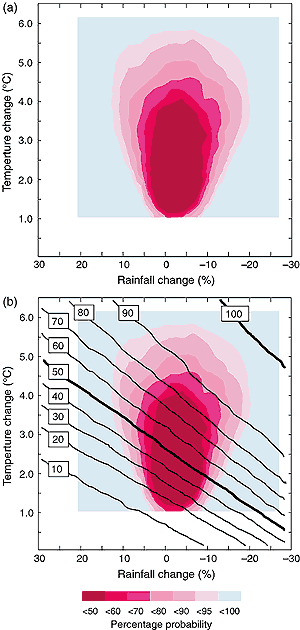
Figure 13.9: (a) Projected ranges of regional annual temperature
and rainfall change for inland southern Australia in 2100 extrapolated
from CSIRO (1996) with temperature sampled randomly across the projected
ranges of both global and normalised regional warming and then multiplied
together. Projected regional ranges for normalised seasonal rainfall change
were randomly sampled, multiplied by the randomly sampled global warming
as above, and then averaged. The resulting probability density surface
reveals the likelihood of different climate change outcomes for this region;
(b) Response surface of irrigation demand for the same region superimposed
on projected climate changes as (a), showing the likelihood of exceeding
an annual allocation of irrigation water supply. Risk can be calculated
by summing the probabilities of all climates below a given level of annual
exceedance of annual water supply; e.g., 50%, or exceedance of the annual
water limit in at least one of every two years. (Source: Jones, 2000b.)
|
|