11.2.1.2 Models of thermal expansion
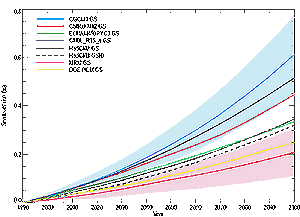
Figure 11.1: Global average sea level changes from thermal expansion
simulated in AOGCM experiments with historical concentrations of greenhouse
gases in the 20th century, then following the IS92a scenario for the 21st
century, including the direct effect of sulphate aerosols.
See Tables 8.1 and 9.1
for further details of models and experiments |
A variety of ocean models have been employed for estimates
of ocean thermal expansion. The simplest and most frequently quoted is the one-dimensional
(depth) upwelling-diffusion (UD) model (Hoffert et al., 1980; Wigley and Raper,
1987, 1992, 1993; Schlesinger and Jiang, 1990; Raper et al., 1996), which represents
the variation of temperature with depth. Kattenberg et al. (1996) demonstated
that results from the GFDL AOGCM could be reproduced by the UD model of Raper
et al. (1996). Using this model, the best estimate of thermal expansion from
1880 to 1990 was 43 mm (with a range of 31 to 57 mm) (Warrick et al., 1996).
Raper and Cubasch (1996) and Raper et al. (2001) discuss ways in which the UD
model requires modification to reproduce the results of other AOGCMs. The latter
work shows that a UD model of the type used in the SAR may be inadequate to
represent heat uptake into the deep ocean on the time-scale of centuries. De
Wolde et al. (1995, 1997) developed a two dimensional (latitude-depth, zonally
averaged) ocean model, with similar physics to the UD model. Their best estimate
of ocean thermal expansion in a model forced by observed sea surface temperatures
over the last 100 years was 35 mm (with a range of 22 to 51 mm). Church et al.
(1991) developed a subduction model in which heat is carried into the ocean
interior through an advective process, which they argued better represented
the oceans with movement of water along density surfaces and little vertical
mixing. Jackett et al. (2000) developed this model further and tuned it by comparison
with an AOGCM, obtaining an estimate of 50 mm of thermal expansion over the
last 100 years.
The advantage of these simple models is that they require less computing power
than AOGCMs and so the sensitivity of results to a range of uncertainties can
easily be examined. However, the simplifications imply that important processes
controlling the penetration of heat from the surface into the ocean interior
are not reproduced and they cannot provide information on the regional distribution
of sea level rise. The most satisfactory way of estimating ocean thermal expansion
is through the use of AOGCMs (Chapter 8, Section
8.3) (Gregory, 1993; Cubasch et al., 1994; Bryan, 1996; Jackett et al.,
2000; Russell et al., 2000; Gregory and Lowe, 2000). Improvements over the last
decade relate particularly to the representation of the effect on mixing by
processes which operate on scales too small to be resolved in global models,
but which may have an important influence on heat uptake (see Section
8.5.2.2.4). The geographical distribution of sea level change due to density
and circulation changes can be obtained from AOGCM results (various methods
are used; see Gregory et al., 2001). The ability of AOGCMs to simulate decadal
variability in the ocean interior has not yet been demonstrated adequately,
partly because of the scarcity of observations of decadal variability in the
ocean for testing these models. This is not only an issue of evaluation of model
performance; it is also relevant for deciding whether observed trends in sea
level and interior ocean temperatures represent a change which is significantly
larger than the natural internal variability of the climate system.
| Table 11.2: Rate and acceleration
of global-average sea level rise due to thermal expansion during the 20th
century from AOGCM experiments with historical concentrations of greenhouse
gases, including the direct effect of sulphate aerosols. See Tables
8.1 and 9.1 for further details of models
and experiments. The rates are means over the periods indicated, while a
quadratic fit is used to obtain the acceleration, assumed constant. Under
this assumption, the rates apply to the midpoints (1950 and 1975) of the
periods. Since the midpoints are 25 years apart, the difference between
the rates is 25 times the acceleration. This relation is not exact because
of interannual variability and non-constant acceleration. |
 |
| |
Rate of sea level rise
(mm/yr)
|
|
Acceleration
(mm/yr/century)
|
 |
| |
1910a to 1990b
|
1960 to 1990b
|
1910a to 1990b
|
| CGCM1 GS |
0.48
|
0.79
|
0.7 0.2
|
| CGCM2 GS |
0.50
|
0.71
|
0.5 0.3
|
| CSIRO Mk2 GS |
0.47
|
0.72
|
1.1 0.2
|
| CSM 1.3 GS |
0.34
|
0.70
|
1.2 0.3
|
| ECHAM4/OPYC3 GS |
0.75
|
1.09
|
1.0 0.5
|
| GFDL_R15_a GS |
0.59
|
0.97
|
1.4 0.4
|
| GFDL_R15_b GS |
0.60
|
0.88
|
1.1 0.3
|
| GFDL_R30_c GS |
0.64
|
0.97
|
1.2 0.3
|
| HadCM2 GS |
0.42
|
0.60
|
0.8 0.2
|
| HadCM3 GSIO |
0.32
|
0.64
|
1.3 0.4
|
| DOE PCM GS |
0.25
|
0.63
|
0.8 0.4
|
 |
A number of model simulations of the 20th century (Table
9.1) have recently been completed using realistic greenhouse gas and aerosol
forcings. Results for global average thermal expansion over periods during the
20th century are given in Figure 11.1 and Table
11.2. They suggest that over the last hundred years the average rate of
sea level rise due to thermal expansion was of the order of 0.3 to 0.7 mm/yr,
a range which encompasses the simple model estimates, rising to 0.6 to 1.1 mm/yr
in recent decades, similar to the observational estimates (Section
11.2.1.1).
| Table 11.3: Some physical characteristics
of ice on Earth. |
 |
| |
Glaciers |
Ice caps |
Glaciers and ice capsa |
Greenland ice sheetb |
Antarctic ice sheetb |
| Number |
>160 000 |
70 |
|
|
|
| Area (106 km2) |
0.43 |
0.24 |
0.68 |
1.71 |
12.37 |
| Volume (106 km3) |
0.08 |
0.10 |
0.18 0.04 |
2.85 |
25.71 |
| Sea-level rise equivalentd |
0.24 |
0.27 |
0.50 0.10 |
7.2c |
61.1c |
| Accumulation (sea-level equivalent, mm/yr)d |
|
|
1.9 0.3 |
1.4 0.1 |
5.1 0.2 |
 |
|