|
4.4.5. Energy Intensities, Energy Demand, and Structure of Energy Use
Population and GDP assumptions, along with structural change and technological
change that affect energy efficiency and energy costs (and prices), drive the
demand for energy services. Given the different model representations of energy
service demands, in this section final energy use is discussed as a common measurement
point across all SRES models and scenarios. Final energy use per unit economic
activity, that is, energy intensity, is a frequently used measure of comparative
efficiency of resource use, and reflects a whole range of structural, technological,
and lifestyle factors (Schipper and Meyers, 1992).
|
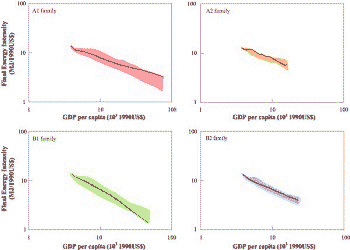
| Figure 4-6: Relationship between final energy
intensity and per capita income in the four marker scenarios. The data points
represent values in 1990, 2020, 2050, and 2100. The 1990 value is at the
top of each curve and the 2100 value at the bottom. |
Figure 4-6 illustrates the evolution of final energy
intensities for the four SRES marker scenarios. Instead of time, per capita
income is shown on the horizontal axis, to illustrate a conditional convergence
of regional final energy intensities. Invariably, intensities are projected
to decline with increasing income levels. As discussed in Chapter
3, the main reason for this trend stems from the common source of economic
growth and energy intensity improvements - technological change. All else being
equal, the faster intensity improvements are, the faster aggregate productivity
(per capita income) grows. An important methodologic improvement over previous
studies is the explicit inclusion of non-commercial energy forms in some SRES
models, drawing on estimates as reported in IPCC WGII SAR (Watson et al., 1996)
and in Nakicenovic et al. (1998).
In the A1 and B1 scenarios, per capita income differences are substantially
narrowed and convergent because of increased economic integration and rapid
technological change. Therefore, differences in energy intensities are also
narrowed significantly and are convergent, as shown in Figure
4.6. The B1 storyline describes a development path to a less material-intensive
economy. Hence, the final energy intensities in the B1 marker are lowest among
the four SRES marker scenarios for a given per capita income level. The A2 storyline
reflects a world with less rapid technological change, as shown by the smallest
rate of energy intensity improvement among the four marker scenarios25.
Different interpretations of the four scenario storylines, as well as alternative
rates of energy intensity improvement to the four marker scenarios, are discussed
below.
Owing to methodologic differences across the six models (see Box
4-7) it is not possible to disaggregate energy intensity improvements into
various components, such as structural change, price effects, technological
change, etc., in a consistent way. In some models (macro-economic) price effects
are differentiated from "everything else" (frequently labeled AEEI, or autonomous
energy intensity improvements). As a rule, the importance of non-price factors
is an inverse function of the time horizon considered. Over the short-term,
the impacts of economic structural change and technology diffusion are necessarily
low. Hence, prices assume a paramount importance in driving alternative energy
demand patterns in short-term (to 2010-2020) scenario studies (e.g., IEA, 1998;
EIA, 1997, 1999). Over the longer term (i.e., the time horizon considered by
the SRES scenarios), economic structural and technological changes become more
pronounced, as does their influence on energy intensity improvements and energy
demand. This does not imply that prices do not matter over the long term, but
simply that "everything else" (e.g., AEEI) is likely to outweigh the impacts
of prices, as indeed suggested by quantitative scenario analyses performed within
the Energy Modeling Forum EMF-14 (Weyant, 1995).
|
Box 4-7: The Role of Prices in SRES Scenarios
The price of energy comprises many components:
- Costs to establish and maintain the production, conversion, transport,
and distribution infrastructure of energy supply.
- Profit margins.
- A whole host of levies such as royalties and taxes raised at the points
of energy production or use.
- Consumers' willingness to pay for quality and convenience of energy
services.
Furthermore, given the importance of energy and the vast volumes traded,
prices are influenced by a whole range of additional factors, from inevitable
elements of speculation to geopolitical considerations, all of which can
decouple energy price trends from any underlying physical balance between
supply and demand. Taxes are especially significant. In a number of OECD
countries, up to 80% of the consumer price of gasoline is taxes (OECD,
1998), and the differences between countries are enormous. In 1997, 27%
of the price of gasoline in the USA was taxes, compared with 78% in France.
Taxes vary substantially even between large oil producers (and exporters).
In Mexico taxes are 13% of gasoline prices, but in Norway they are 75%
(OECD, 1998).
Currently, no methodologies exist to project future energy prices taking
all of above mentioned factors into account, nor were the SRES scenarios
intended to make explicit assumptions on such factors such as future energy
taxation. Price information enters long-term emission models either in
the form of exogenous scenario assumptions, or it is derived internally
in models based on simplified representations of price formation mechanisms
usually based on (marginal) cost information.
The six models used for SRES range from detailed "bottom-up" models (e.g.,
AIM, IMAGE), through macro-economic (partial equilibrium) models (e.g.,
MARIA, MiniCAM), to hybrid approaches (successive iteration between the
engineering model MESSAGE with a macro-economic model, or using the Worldscan
model with IMAGE). Each has different representations of price formation
mechanisms and their relationship to macro-economic or sectoral energy
demand. These are summarized in Appendix IV.
As a rule, "bottom-up" (optimization) models calculate only (average and
marginal) costs endogenously. As a result of their sectoral perspective
(energy, agriculture, etc.), these models cannot determine macro-economic
feedbacks on other sectors or the entire economy and thus are unable to
represent a consistent picture of price formation. Conversely, price formation
is endogenized in "top-down" models; however, these rely on the stringent
assumption that demand and supply must be in equilibrium and in addition
provide little sectoral detail. Over recent years this simplified modeling
dichotomy has progressively weakened because of further advances in methodology
and the development of "hybrid" modeling approaches. To illustrate the
methodologies deployed in the six SRES models, two (MARIA and MESSAGE)
are discussed here, but (for space limitations) only in terms of one scenario
(B2). (Table 4-9 gives additional details of an inter-scenario
comparison of energy prices for the MiniCAM and ASF models. Owing to methodologic
differences, a comparison of prices across scenarios is only possible
within a consistent approach (i.e. be comparing scenarios quantified with
the same model).)
The energy prices represented in MARIA (see also Mori, 2000) consist
of energy production and energy utilization costs. Market prices are determined
endogenously by model-calculated shadow prices (for further model details
see Appendix IV and Mori and Takahashi, 1999). Among various parameters,
the extraction costs of fossil fuel resources and the coefficients of
utilization costs and their evolution over time are the most important
determinants. For the MARIA runs, the resource estimates of Rogner (1997)
were used as input. For the sake of simplicity, all fossil resource categories
of Rogner (1997) were aggregated into two classes and a quadratic production
function was used to interpolate the extraction costs of reserves and
all other occurrences. For coal, long-term extraction costs range up to
US$6.3 per GJ in 1990US$ prices, for gas up to US$25 per GJ, and for oil
up to US$28 per GJ (see Appendix IV for further details). The energy cost
coefficients (representing 16 different energy conversion technologies)
are based on Manne and Richels (1992). For the B2 scenario quantification,
the Manne and Richels (1992) estimates were largely retained. For instance,
electricity generation costs range between 14 mills26
/kWh for gas to 51 mills/kWh for coal. (For the other scenario quantifications
these cost values were modified to conform to the different interpretations
of a particular scenario storyline.) Together these assumptions determined
long-run costs and shadow prices that were set equal to energy prices
in the macro-economic production function of MARIA. The energy prices
were combined with assumed (low) AEEI values and potential GDP growth
rates (the latter from the B2 marker) to calculate the resultant aggregate
energy demand in the model. The resultant primary energy demand was (with
exception of the REF region) within 15% of the respective B2 marker quantification
at the regional level and within 5% of global energy demand. As a result
of different model structures, comparable price data for the MESSAGE model
are only available for internationally traded primary energy forms (these
are given in Table 4-8).
The bottom-up, systems engineering (optimization) model MESSAGE does
not compute energy prices. Instead, the model is entirely based on cost
information, but such costs are treated as dynamic. Their overall treatment
follows the lines outlined above for the MARIA model, except that greater
technology-specific detail is contained in the model. Altogether 19 different
fossil resource grades are differentiated, based on the estimates of Rogner
(1997). The resultant (levelized) extraction costs for the B2 marker are
in the range US$1.1 to US$5.4 per GJ for coal, US$1.2 to US$5.3 per GJ
for oil, and US$1.2 to US$5.7 per GJ for gas (range indicates costs variations
between lowest and highest costs of the four SRES regions for 2020, 2050,
and 2100 respectively, see Appendix IV). Technology-specific cost assumptions
cannot be summarized here as MESSAGE contains literally hundreds of energy
supply and end-use technologies. Examples of cost assumptions are given
in Section 4.4.7 and more detail is reported in
Riahi and Roehrl (2000). However, as in MARIA, MESSAGE also calculates
shadow prices for internationally traded primary energy forms and therefore
these two indicators can be compared (Table 4-8).
|
Important feedback mechanisms between technological change and costs (and thus
also prices) exist over the long term. These are as a rule treated endogenously
in the models, for instance when modeling long-run resource extraction costs
or structural changes in energy supply options (see Sections 4.4.6
and 4.4.7). Energy prices are also strongly affected by
policies (e.g., taxation), but to project these far into the future is both
outside the capability of currently available methodologies and outside the
general "policy neutral" stance of the SRES scenarios. Therefore, most models
treat dynamic changes in (average and marginal) costs as the driving
force for energy intensity improvements and for technology choice (see Sections
4.4.6 and 4.4.7).
4.4.5.1. A1 Scenarios
Improvements in energy efficiency on the demand side are assumed to be relatively
low in the A1B marker scenario, because of low energy prices caused by rapid
technological progress in resource availability and energy supply technologies
(see Sections 4.4.6 and 4.4.7).
These low energy prices provide little incentive to improve end-use-energy efficiencies
and high income levels encourage comfortable and convenient(and often energy
intensive) lifestyles (especially in the household, service, and transport sectors).
Efficient technologies are not fully introduced into the end-use side, dematerialization
processes in the industrial sector are not well promoted, lifestyles become
energy intensive, and private motor vehicles are used more in developing countries
as per capita GDP increases. Conversely, fast rates of economic growth and capital
turnover and rising incomes also enable the diffusion of more efficient technologies
and economic structural changes, with consequent improvements in energy intensity.
As a result, the rate of energy intensity improvement in Annex I countries is
around 1.16% per year, and in non-Annex I countries 1.44% over the 100 years
to 2100. Thus, final energy use for A1 is much higher than those in the A2,
B1, and B2 scenarios, with a substantial long-term convergence in final energy
use per capita between Annex 1 countries and non-Annex 1 countries.
| Table 4-8: International price
(MARIA) and calculated shadow price (MESSAGE) of internationally traded
energy (1990US$/GJ) by 2020, 2050, 2100 for the SRES B2 scenario. |
|
|
Coal
|
|
Oil
|
|
Gas
|
|
Biofuels
|
Synfuels
|
|
|
MARIA |
MESSAGEa |
MARIA |
MESSAGEb |
MARIA |
MESSAGEc |
MARIA |
MESSAGEd
|
|
| 2020 |
0.5
|
3.4
|
3.5
|
3.9-4.4
|
2.9
|
2.8-4.4
|
4.8
|
n.a.
|
| 2050 |
0.8
|
2.5
|
4.9
|
7.5-8.2
|
4.3
|
5.1-6.4
|
6.5
|
10.4-16.2
|
| 2100 |
1.4
|
8.1
|
6.3
|
17.3-18.2
|
5.4
|
5.2-11.4
|
6.3
|
17.1-20.7
|
|
|
A.
Costs include export and/or import infrastructure and transport.
B. Range between crude oil and light and heavy oil products.
C. Range between liquid natural gas and direct pipeline imports to North
America, Europe, Japan, and North Africa.
D. Range between methanol, ethanol, and liquid hydrogen.
To achieve consistency between model-calculated energy cost dynamics
and energy demand assumptions an iterative modeling procedure between
MESSAGE and MACRO (a macro-economic production function model based on
Manne and Richels, 1992) was used, on the basis of model-calculated shadow
prices as indicators of future price dynamics. The methodology is described
in more detail in Wene (1996). This approach requires time-intensive model
iterations, but has the advantage that the impact of price increases can
be separated from efficiency improvements through fuel substitution (e.g.,
a gas-fired cook stove energy end-use efficiency is up to 10 times higher
than a traditional cook stove fired with fuelwood) as well as from "everything
else," i.e., the AEEI in the traditional sense). Aggregated, the impact
of (shadow) price increases in MESSAGE's B2 scenario accounts for 8% of
global primary energy demand by 2020, 23% by 2050, and 30% by 2100. This
impact is calculated as a reduction in energy demand compared to a hypothetical
scenario with constant 1990 prices (and correspondingly higher energy
demand). The impact of price increases on future energy demand in the
B2 scenario is thus relatively small compared to that of other factors,
although far from negligible. This also explains why the two B2 scenario
quantifications by MARIA and MESSAGE have quite similar energy demand
figures, even if international trade prices may differ. First, trade prices
are only one component of the cost-price mechanism treated in the models
(which also includes domestic energy production, conversion, and end-use
costs). Second, models differ in their parametrizations of the "everything
else" (AEEI) model parameters, for which a wide range of views on applicable
ranges exists. Therefore it is one of the model calibration parameters
frequently used to replicate existing scenarios or to standardize inter-model
comparison projects such as EMF-14 (Weyant, 1995).
|
| Table 4-9: Energy prices (1990US$/GJ)
across SRES scenarios as calculated in the ASF (top) and MiniCAM models
for their respective A1, A2, B1, and B2 (cf. Table 4-8)
scenarios. Note in particular significant base-year differences in fuel
prices because of different cost accounting definitions used in models (c.i.f.
versus f.o.b.27
), in particular with respect to transportation costs (included in the price
figures given for ASF, but excluded in the numbers given for MiniCAM). |
|
| |
|
A1 |
A2 |
B1 |
B2 |
|
| ASFa |
|
|
|
|
|
| Coal |
2000
2020
2050
2100
|
1.5
1.6
1.9
2.0 |
1.5
1.5
1.7
1.8 |
1.5
1.6
1.7
1.6 |
1.5
1.5
1.6
1.7 |
| Oil |
2000
2020
2050
2100 |
4.4
5.3
7.1
7.7 |
4.4
4.7
6.2
7.5 |
4.4
5.1
6.3
6.1 |
4.4
4.7
6.1
7.1 |
| Gas |
2000
2020
2050
2100 |
5.0
5.0
5.3
7.9 |
5.0
5.0
5.0
6.1 |
5.0
4.9
4.8
4.9 |
5.0
5.0
4.9
5.8 |
| MiniCAMb |
|
|
|
|
|
| Coal |
1990
2020
2050
2100 |
1.0
1.6
1.9
2.5 |
1.0
1.7
2.0
2.5 |
1.0
1.6
1.7
1.9 |
1.0
1.6
1.7
2.0 |
| Oil |
1990
2020
2050
2100 |
3.9
8.6
10.4
9.6 |
3.9
10.2
13.3
15.2 |
3.9
6.4
9.9
8.5 |
3.9
7.3
10.4
10.2 |
| Gas |
1990
2020
2050
2100 |
1.6
2.8
3.8
6.8 |
1.6
3.2
5.7
8.7 |
1.6
2.0
2.5
1.9 |
1.6
2.4
3.0
2.3 |
| Biofuels |
1990
2020
2050
2100 |
n.a.
2.1
2.4
2.3 |
n.a.
2.2
2.6
3.2 |
n.a.
2.0
2.0
1.5 |
n.a.
2
2.1
2.0 |
|
A.
ASF: global average supply price, including transportation.
B. MiniCAM: as determined by solution to a partial equilibrium supply and
demand model. |
|